OpenSim Moco  0.4.0
Public Member Functions | Protected Attributes | List of all members
CasOC::Endpoint Class Reference

Description

This function takes initial states/controls, final states/controls, and an integral.

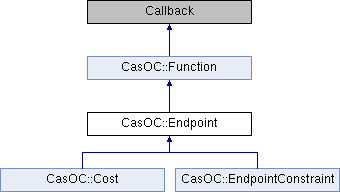
Inheritance diagram for CasOC::Endpoint:
CasOC::Function CasOC::Cost CasOC::EndpointConstraint

#include <Moco/Moco/MocoCasADiSolver/CasOCFunction.h>

Public Member Functions

void constructFunction (const Problem *casProblem, const std::string &name, int index, int numEquations, const std::string &finiteDiffScheme, std::shared_ptr< const std::vector< VariablesDM >> pointsForSparsityDetection)
 
casadi_int get_n_in () override
 
std::string get_name_in (casadi_int i) override final
 
casadi::Sparsity get_sparsity_in (casadi_int i) override
 
casadi_int get_n_out () override final
 
std::string get_name_out (casadi_int i) override final
 
casadi::Sparsity get_sparsity_out (casadi_int i) override final
 
casadi::DM getSubsetPoint (const VariablesDM &fullPoint) const override
 The endpoint input is not simply a subset of the NLP variables; the endpoint function also depends on an integral, computed from an integrand function and using a transcription's quadrature scheme. More...
 
- Public Member Functions inherited from CasOC::Function
void constructFunction (const Problem *casProblem, const std::string &name, const std::string &finiteDiffScheme, std::shared_ptr< const std::vector< VariablesDM >> pointsForSparsityDetection)
 
void setCommonOptions (casadi::Dict &opts)
 
std::string getFiniteDifferenceScheme ()
 
casadi_int get_n_in () override
 
std::string get_name_in (casadi_int i) override
 
casadi::Sparsity get_sparsity_in (casadi_int i) override
 
bool has_jacobian_sparsity () const override
 
casadi::Sparsity get_jacobian_sparsity () const override
 

Protected Attributes

int m_index = -1
 
int m_numEquations = -1
 
- Protected Attributes inherited from CasOC::Function
const Problem * m_casProblem
 

Member Function Documentation

◆ getSubsetPoint()

casadi::DM CasOC::Endpoint::getSubsetPoint ( const VariablesDM &  fullPoint) const
inlineoverridevirtual

The endpoint input is not simply a subset of the NLP variables; the endpoint function also depends on an integral, computed from an integrand function and using a transcription's quadrature scheme.

Ideally, the value for the integral would be computed properly from the provided point, but applying the integrand function and quadrature scheme here is complicated. For simplicity, we provide the integral as 0.

Reimplemented from CasOC::Function.

The documentation for this class was generated from the following file: